投稿日:2022年3月1日

部品の寸法が図面通りできているか確認するためには必ず測定を行います。その測定結果がどれだけ正しいか気にしたことはあるでしょうか。
高価な測定器を使って測定した結果は、正しいものだと思うかもしれません。しかし、測定した結果には、必ず不確かさがあります。そして不確かさは、測定器に付いているものではなく、測定結果に付くものです。
つまり、同じ測定器を使っていても、測定条件、測定環境、測定した人など様々な要因で不確かさは変化します。
不確かさを理解せずに測定をしていると、測定の不確かさが大きくなってしまいます。測定の不確かさが大きいと、測定するたびに測定結果が変わったり、正しい測定結果との差が大きくなったりします。それによって、部品の品質が保証できなくなってしまうのです。
したがって、測定の不確かさを理解することが部品の品質保証をするうえで重要になります。
測定の不確かさの重要性:誤差は神様にしかわからない
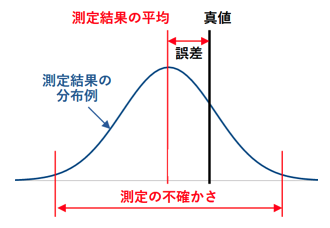
測定結果の正しさを表す言葉として、昔から「誤差」が使われてきました。現在も使っている人が多いと思います。
測定の世界で、「誤差」とは真の値と測定値との差です。つまり真の値がわかることが前提になっています。しかし、私たちが知りえる情報には限りがあるため、真の値を知るということは不可能です。そこで最近では、「不確かさ」という考え方が主流になっています。
測定の不確かさとは、測定された結果がどれだけ信用できるかを数値化したものです。
例えば、
99.95 mm ± 0.10 mm (信頼の水準95%)
であれば、99.95 mmが測定結果で、0.10 mmの部分が不確かさです。
測定した寸法は、95%の確率で、99.85 mmから100.5 mmの間にあるという意味です。
このように、不確かさを表記することで「真の値」が、「どのくらいの範囲」の中に「どのくらいの確率」で存在するかがわかるようになります。よって、測定結果の信頼性を示すために、不確かさは重要な役割を担っています。
不確かさによって、部品の寸法が合格の範囲に入っているかをより正確に判断できます。
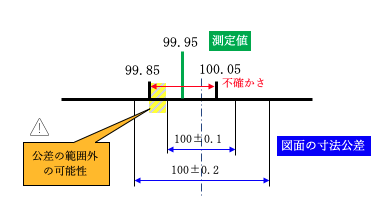
上記の例で、部品の寸法公差が100 mm ± 0.2 mmと指定されている場合は合格です。しかし、100 mm ± 0.1 mmと指定されている場合は不合格です。部品の寸法が公差の範囲外である、99.85~99.90 mmの可能性があるからです。
しかし、不確かさが表示されていない場合、99.95 mmという測定結果のため、合格になってしまいます。これでは、不合格品を合格品として出荷してしまう可能性があります。
このように、不確かさを考慮することで、品質管理をより正確に行えるようになります。
また、より良い測定を行うためには、不確かさを小さくする必要があります。不確かさを評価することによって、不確かさが大きくなる要因を特定できます。
その要因を改善することで、不確かさの小さい、より良い測定ができるようになります。
不確かさは「かたより」と「ばらつき」からできている
不確かさは、主に「かたより」と「ばらつき」を計算して求めます。
ここでは、「かたより」と「ばらつき」について解説します。
かたよりはいつも起きる
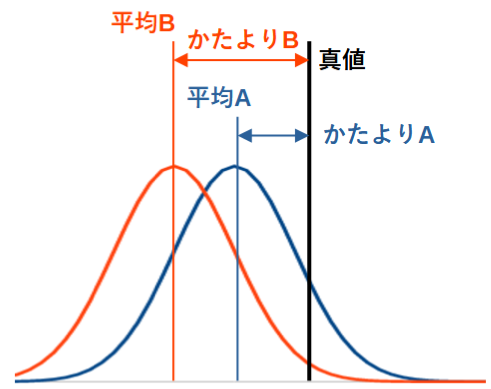
かたよりとは、「真の値」と「測定結果の平均」との差です。
何かしらの原因で、測定結果が真の値より大きく出たり、小さく出たりします。
「この体重計は自宅の体重計と比べて、いつも1 kg重く表示される」とか、「温度計Aと温度計Bでは同じ室温を測定しても、いつも0.1 ℃ 違う」といった経験があると思います。それは、体重計や温度計にかたよりがあるからです。
上の図では、平均Aより平均Bの方がかたよりが大きいと言います。かたよりが大きいほうが不確かさが大きくなります。
真の値がある程度わかっている場合には、補正することによって、かたよりを小さくすることが可能です。よって、より良い測定を行う場合には、可能な限りかたよりの要因の特定し、補正する必要があります。
ばらつきは偶然で起きる
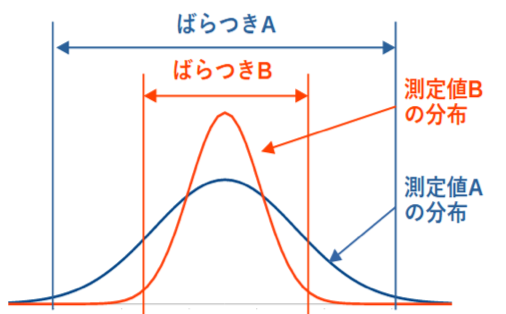
ばらつきとは、測定結果が分布する幅のことを言います。
上図では、測定値Bより測定値Aの方がばらつきが大きいと言います。ばらつきが大きいほうが不確かさが大きくなります。
ばらつきは偶然起きるため、補正することができません。ばらつきを小さくするには、ばらつきの原因を突き止める必要があります。測定条件の変更や、人員の教育というソフト面で改善される場合もあります。
また、測定器を高性能なものに変えたり、測定環境を整えたりとハード面の改善をしなくてはいけない場合もあります。ばらつきをどこまで小さくするかは、コストとの兼ね合いになります。
不確かさの計算は二乗和の平方根
不確かさの計算(見積もりという)手順は以下の通りです。
- 思いつく限り不確かさの要因の挙げます。
- それぞれの要因に対して、不確かさへの影響を計算、または測定してunを求めます。
- 不確かさへの影響が大きい要因だけを抽出します。
- 抽出されたunを二乗和の平方根により合成し、合成標準不確かさuを求めます。
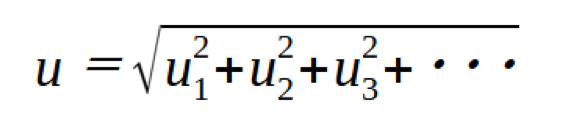
不確かさの要因の数や種類には正解がありません。過不足なく挙げられていればOKです。自己申告制のため、技術力の無い企業は、不確かさの要因が思いつかず、不確かさは小さくなってしまいがちです。
しかし、実際の実力より不確かさが小さいと、「過小評価」といって社会的信用を失います。不確かさの過小評価にならないよう、注意が必要です。
具体的な不確かさの見積もりを知りたいという方は、
JCSS公開文書一覧というサイトもあるので、参考にすると良いでしょう。また、新しいJISでは不確かさの指針を追加する傾向があります。
最新のJISを確認するのも良いでしょう。ただし、何度もいいますが、不確かさの見積もりに正解はありません。多くの人が納得できる内容であればOKです。
包含係数で不確かさの信頼度がわかる

測定器の仕様書などを見ると測定器の精度の所に、暗号のように「k=2」と書かれていることがあります。kとは「包含係数」を意味し、 k=2は不確かさの「信頼の水準」が95%であることを意味します。ちなみに、k=1は68%、k=3は99.7%の信頼の水準です。
詳細の説明は避けますが、
U=ku
で計算されます。
Uは拡張不確かさ、uは前章で計算した合成標準不確かさです。
つまり、 k=2とは計算した不確かさを2倍することで、不確かさの信頼性を95%にしているんだなと思えば問題ありません。
まとめ
不確かさは比較的新しい考え方なので、まだ採用していない職場や、不確かさを知らない上司も多いと思います。
しかし、世界的には不確かさの重要性が広まってきており、ISOやJISなど規格の整備が進められています。
最先端の技術の製造に関わっている場合は、不確かさの影響が小さくありません。良いものが安定して造れないといった場合には、測定の不確かさを確認してみましょう。本当に狙った寸法で造られているのか、たまたま狙った数値が出ただけなのかがわかります。
正しい不確かさの計算には、トレーサビリティが欠かせません。
トレーサビリティについての詳しい記事は【品質保証】長さのトレーサビリティについてをご参照ください。















