投稿日:2022年3月26日

ものづくりをする際に、必ずといっていいほど行う作業に寸法測定があります。
寸法測定をした結果が正しいと思っているかもしれませんが、測定にはさまざまな要因で誤差が生じます。そしてその誤差の大きさは測定器の機構によっても大きく左右されます。
精度良く測定したいなら、「アッベの原理」を満たした測定器を使用する必要があります。アッベの原理は非常に簡単な原理なので、慣れてくれば見ただけでアッベの原理を満たしているのかいないのか見分けることができます。
しかし、アッベの原理が理解できていないと要求する精度を満たしていない測定器を使って測定してしまうことになりかねません。
また、アッベの原理は測定器を利用するときに必要なだけではありません。装置を設計するときに、アッベの原理を意識するかどうかで装置の精度が1桁2桁変わることもあります。
ぜひアッベの原理を理解して、装置設計に役立てましょう。
アッベの原理とは
ノギスの最小目盛は0.05~0.02 mmなのに対して、マイクロメータの最小目盛は0.01~0.001 mmなのはなぜか考えたことはありますか?
実は、ただのデザインでそうなっているわけではありません。マイクロメータの方が精度良く測定できる原理にのっとって作られているからです。
精度良く測定できる原理というのが、「アッベの原理」です。有名な原理なので、一度は聞いたことがあるかもしれませんが、正しく理解しているでしょうか?
アッベの原理とは、「測定対象物と測定器の目盛りを一直線上に配置した方が精度良く測定できる」という原理です。
文で書くと非常にシンプルですが、わかりにくいと思うので、具体的な例を見てみましょう。
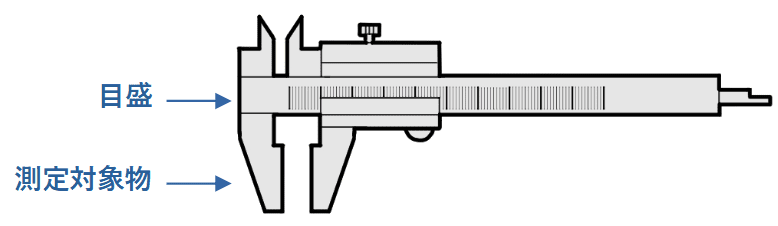
まずはノギスについて見てみます。図からもわかるように目盛りと測定対象物の位置が一直線ではありません。つまり、ノギスはアッベの原理を満たしていない測定器です。
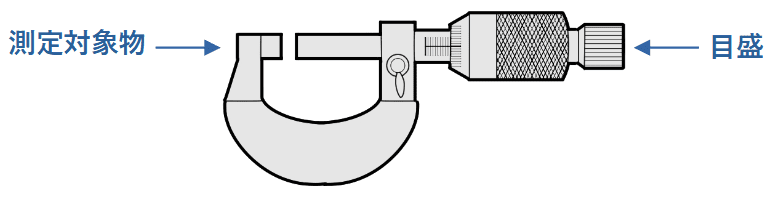
つぎにマイクロメータについて見てみます。図を見てわかる通り、測定対象物と目盛りが一直線上に配置されています。つまり、マイクロメータはアッベの原理を満たしている測定器です。
このように、マイクロメータはアッベの原理を満たしているので、ノギスと比べて精度が高い測定器です。しかし、なぜアッベの原理を満たしていると精度良く測定ができるのでしょうか。
コサイン誤差で誤差を小さくする
ノギスであれ、マイクロメータであれ測定器の多くは、測定物を挟む為に測定器の可動部がスライドします。スライドするということは、部品同士の間にスキマがあるということです。
このスキマは非常に小さいのですが、このスキマが測定に大きく影響します。
アッベの原理を満たさない場合
例えば、ノギスのように測定対象物と目盛りが一直線にない場合を考えます。
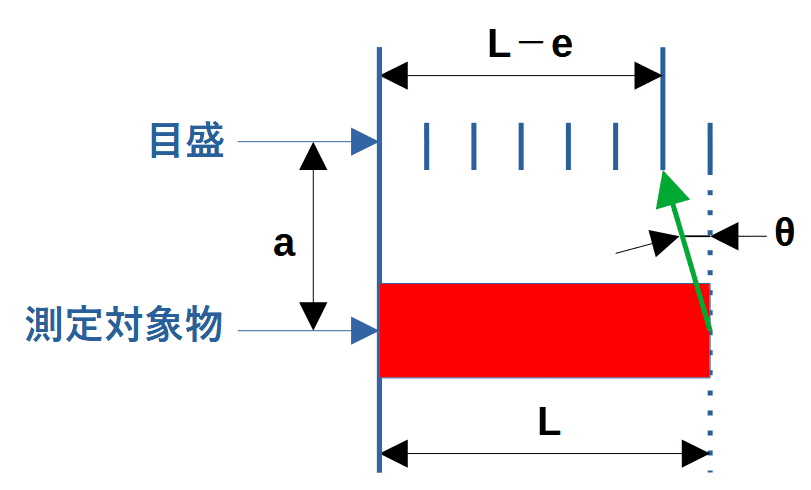
図のように測定対象物と目盛りの間に距離aだけズレがあるとします。角度θのスキマがあって目盛りの指示がeだけずれると、実際の長さがLのものが、長さL+eとして測定されます。
つまりeだけ誤差が生まれます。
この誤差eを式で表すと下式のようになります。
e=a tan θ
θが微小の場合は、
tan θ ≒ θ
となるので、
e=a θ
と表すことができます。
つまり、誤差eは距離aと角度θに比例して大きくなります。
アッベの原理を満たす場合
次に、マイクロメータのように測定対象物と目盛りが一直線の場合を考えます。
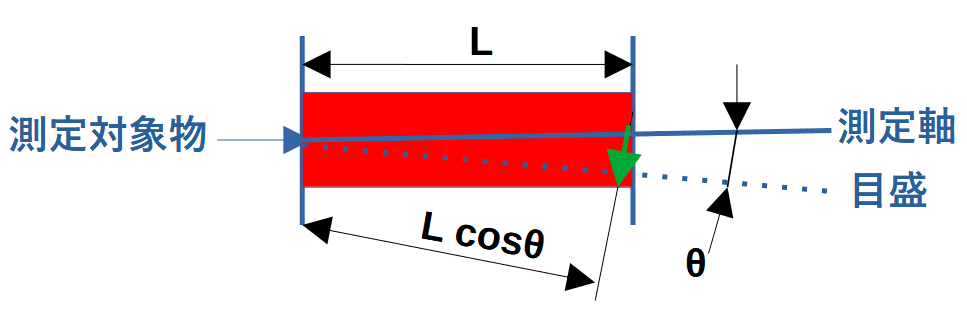
図のように目盛りの軸と測定軸が角度θだけずれた場合、測定結果はL cos θとなるので、誤差eは、
e=L-L cos θ = L(1-cos θ)
で表されます。
cos θをテイラー展開して、θを微小とすると
cos θ =1-θ2 /2
となるので、
e= L(1-(1-θ2 /2))= L(θ2 /2)
となります。
θは微小なので、θ2は極微小になり、誤差eはとても小さな値になります。
アッベの原理を満たしていると、誤差がコサインに比例するので、「コサイン誤差」と呼ぶことがあります。
具体的な数値で計算
数式が多くなってしまいましたが、具体的な数値で見てみるとよくわかります。
例えば、
- L=100 mm
- a=10 mm
- θ=0.01 rad
だとすると、ノギスの場合、
誤差e=a θ = 10×0.01=0.1 mm
と計算できます。
一方、マイクロメータは、
誤差e=L(θ2 /2) = 100×(0.01×0.01/2)=0.005 mm
と計算できます。
この例のように、ノギスは0.1 mm程度の誤差があるので、最小目盛が0.05~0.02 mmとなっており、これ以上小さくしても誤差に埋もれて意味がありません。
一方のマイクロメータは誤差が0.005 mm程度と小さいので、最小目盛を0.01~0.001 mmまで小さくする意味があるのです。
アッベの原理を使った機械設計
アッベの原理は、測定の誤差を小さくするのに有効なのは分かったと思いますが、測定器以外にも多くの実用ができます。精密位置決めステージを設計することを例に考えてみましょう。
精密位置決めステージには、モータなどのアクチュエータとリニアスケールなどの位置センサが必要です。
位置センサの位置がアッベの原理を満たすことができれば、非常に高精度な位置決めステージを設計することができます。
例えば一般的な精密位置決めステージを横から見ると下図のようになっています。

本当はステージの上面に載っているサンプルの位置が知りたいのですが、センサの位置と測定したい位置がずれていることがわかります。
ステージが全く傾かなければ正確に測定できますが、実際には動くことで傾いてしまうため、ステージ上面とセンサ位置ではズレが生じます。
アッベの原理を満たしているステージとは下図の通りです。

この図のように、測定したい高さと同じ高さにセンサを配置します。このように設計することによって、仮にステージが傾いてもコサイン誤差の影響しか受けないため、高精度な位置測定ができるようになります。これによって、超精密位置決めが実現できます。
実際に設計してみると、そんな所にセンサを取り付けるスペースがないと思うかもしれません。
しかし、アッベの原理を頭に入れているだけでも、測定したい位置にセンサの位置を近づける意識が生まれます。これにより、いつもより高精度な装置を簡単に実現できます。
まとめ
今回はアッベの原理について紹介しました。アッベの原理を満たした方が、精度良く測定できる理由が分かったのではないでしょうか。
アッベの原理は、測定器だけではなく、装置の設計でも役に立ちます。アッベの原理を上手く活用して、今後の設計に役立てましょう。














